
Let's look at the definition of orthocenter again and applyit here. Now consider what we are trying to prove that A is the orthocenter oftriangle HBC. Segment HC is perpendicular to segment AB. Segment HB is perpendicular to segment AC Segment HA is perpendicular to segment BC We are given that H is the orthocenter of triangle ABC. If H is the orthocenter of triangle ABC, then A is the orthocenterof triangle HBC. Also the point H, the common vertex of the three triangles HAC, HAB,and HBC, is the orthocenter of triangle ABC.
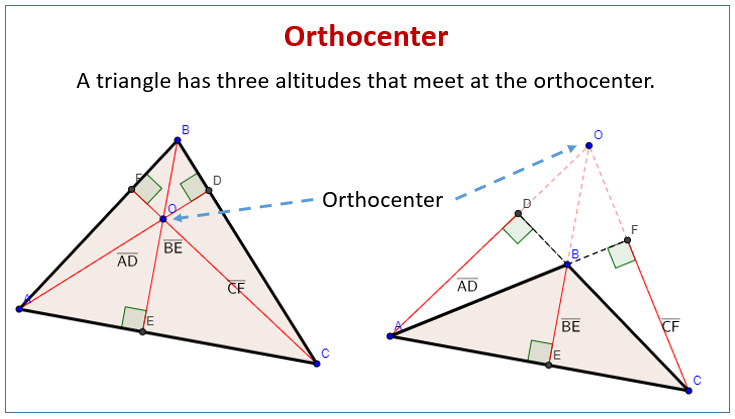
If we look at triangle HAB and HBC individually and construct theirorthocenters, we would find their orthocenters to be vertices of the triangleABC. Furthermore,two more new triangles are formed from this construction, triangles HABand HBC. When the orthocenter B is constructed, a new triangle ABC is also constructedin the process where B is a vertex of this new triangle ABC. Next construct the orthocenter of HAC call it B. Let's also look at what happens when we reverse the order of constructingthe original triangle ABC when the orthocenters for each individual triangleare constructed from the orthocenter of triangle ABC. If our conjectures are true, then the orthocenter of triangle HABshould be C and the orthocenter of triangle HAC should be B.Ĭonstruct the orthocenters of triangles HAB and HAC, respectively, to verify. The most interestingof all is the orthocenter of triangle HBC is A, one of the verticesof the original triangle ABC.ĭoes this same pattern repeat itself when constructing the orthocentersfor triangles HAB and HAC? Similarly,the altitude drawn from C to HB is also segment AC. Also, the altitude from B to HC lieson segment AB, one of the sides of the original triangle ABC. When constructing the orthocenter for HBC, the altitude from H to BC isthe same as the altitude from A to BC. Construct the orthocenter of triangle HBC. Recall theorthocenter of a triangle is the common intersection of the three linescontaining the altitudes.įor a GSP script that constructs the orthocenter of any triangle,click here. Next construct the orthocenter, H, of triangle ABC. Our exploration begins with the following construction:

Are there any relationships between the altitudes and orthocentersof a given set of triangles and the Nine-Point Circle for those same triangles? Can we find interesting mathematical phenomena and make connectionsamong the altitudes and orthocenters of a given set of triangles? 2.
Our exploration centersaround two questions:ġ. We want to investigate the relationships between altitudes and orthocentersand their connections with the Nine-Point Circle. Key thing here was remembering that constructing an altitude is the exact same process as constructing a perpendicular through a point to a line.Altitudes and Orthocenters: Making Connections to the Nine-Point CircleĪlthough the Greeks worked fruitfully, not only in geometrybut also in the most varied fields of mathematics, nevertheless we todayhave gone beyond them everywhere and certainly also in geometry. So now I can connect these, I’m going to label it as a right angle, and I’m going to create point D. We have a point down here and we have B and notice that it says line segment BD, so I’m going to make sure that this is going to end on that side AC. So sharp end is going to be at B and I’m going to extend that a little bit more so I get two points of intersection okay actually it’s a little too much, so I’m going to swing an arc, so now we have our two points of intersection and I need to have, In have one point on this line that’s vertex B and I’m to swing one more arc from each of these end points, so here is one arc.Ĭome over to this point of intersection swing another arc and so now we have our two points. Start off my grabbing your compass and you want to swing an arc with your compass sharp end at B and we want to intersect this side AC twice. To do this construction, we would swing an arc from that point, and then from each of these endpoints we would swing two more arcs and then we would connect these and we would have our perpendicular segment, so that’s what we’re going to do. So an idea of what we’re going to do here is to think of the vertex B as some point in space and we have this opposite side AC. So we’re starting at B and we’re going to some point D on this opposite side. So if I look at this triangle right here, we’re being asked to construct altitude BD, so that tells you the vertex that you’re going to. So in construction remember you’re only using two things a compass and a straightedge, but what is an altitude? Well we said our definition of an altitude is a perpendicular segment from a vertex to the line containing the opposite side. You’re probably going to be asked to construct an altitude in a triangle.


 0 kommentar(er)
0 kommentar(er)
